196

16489 readers

2710 users here now

Be sure to follow the rule before you head out.

Rule: You must post before you leave.

^other^ ^rules^

founded 1 year ago

MODERATORS

[email protected]

QR code rule (lemmy.dbzer0.com)

submitted 2 months ago by [email protected] to c/[email protected]

9 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

[–] [email protected] 0 points 2 months ago* (last edited 2 months ago) (3 children)

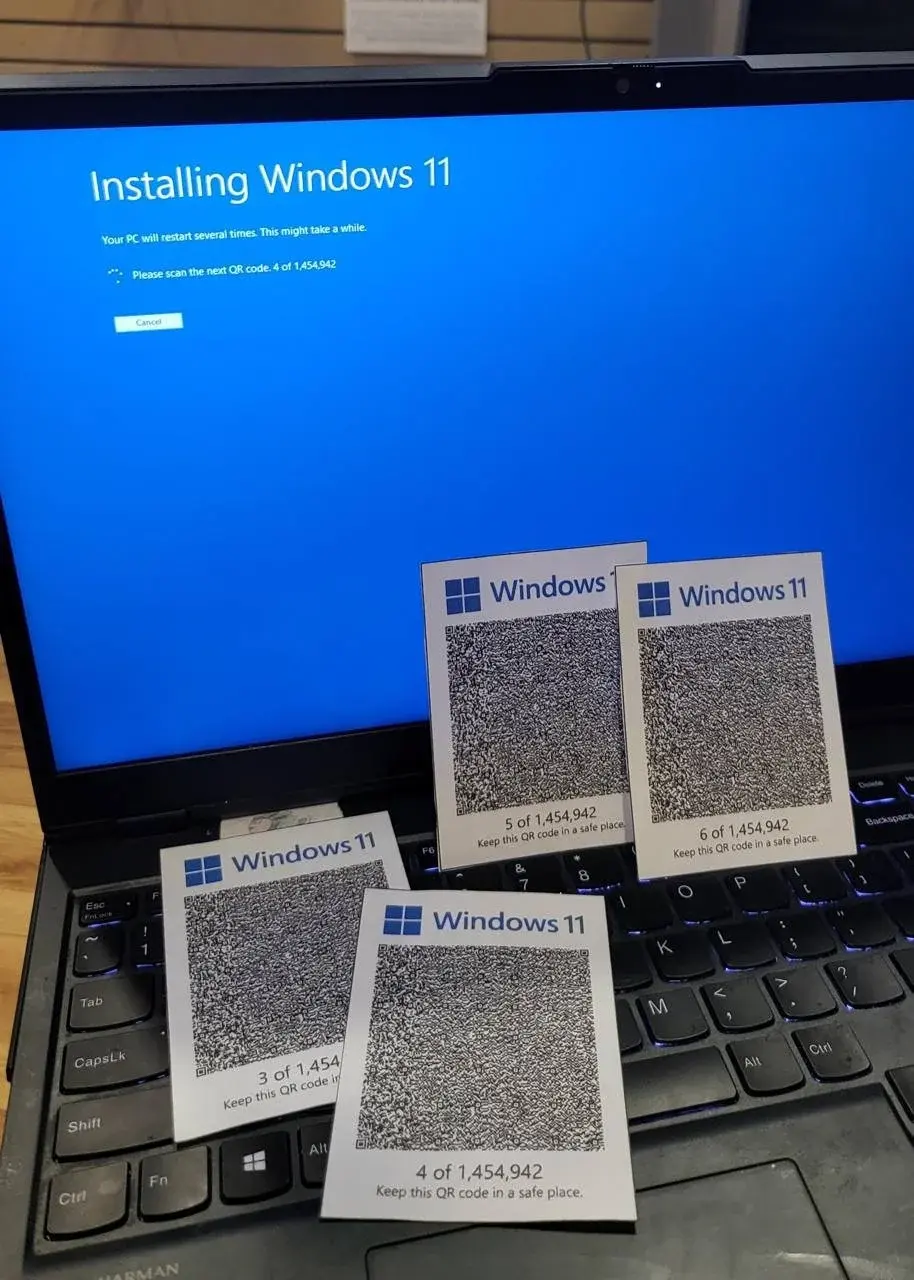
Using 1,454,942 maximum size and minimum error correction QR codes in alphanumeric mode (byte mode is a lie) to store Base64-encoded binary data, you get roughly 4,687,823,124 bytes. 4.6 GB. If the cards are two-sided we get 9.2 GB.

Minimum size of Windows 11 installer image seems to be 8 GB, so it checks out!

[–] [email protected] 2 points 2 months ago (1 children)

Well, here I go printing 1244 pages of QR codes to store tinycorelinux for the after times.

[–] [email protected] 0 points 2 months ago (1 children)

Better figure out how to code a QR reader in pure machine code as well.

[–] [email protected] 1 points 2 months ago

It's cool, you can teach yourself to decode QR by hand

[–] [email protected] 1 points 2 months ago (1 children)

Why Base64? QR codes can contain pure binary data, no need to use this inefficient, not-error-correcting 6-to-8 encoding.

Oh, I forgot Microsoft does not care jack shit about saving people's computing resources. However, Windows 9x installers on floppies used custom formatting except the first bootable one, allowing them to fit nearly 2 MB of useful data per floppy.

[–] [email protected] 0 points 2 months ago* (last edited 2 months ago) (1 children)

They can contain binary data, but less of it. Not sure of the details, but you get 3k bytes if binary data or 4.2k alphanumeric letters. So no big difference all in all, which is a bit silly.

Also, many QR scanners can't handle binary data and freak out on null values or newlines.

We must consider the practical side of installing Windows 11 from a semitrailer load of cardboard.

[–] [email protected] 1 points 2 months ago* (last edited 2 months ago)

The alphanumeric mode does not support lowercase though, it has 5.5 bits/char (pairs of characters are encoded as a base-44 numbers in 11 bits).

[–] [email protected] 0 points 2 months ago (1 children)

Nice!

Though if they were double sided, there is no way we can see all these cards in the same shot. If it starts at odd numbers (i.e. #1), #3 and #4 would share the same card front and back, if it starts even (i.e. a cover graphic and #1 on the same card), #4 and #5 should share the same card front and back.

[–] [email protected] 1 points 2 months ago

Card#1, Card#1 back, Card#2, Card#2 back, etc is what you need to get 9GB out of the 1,454,492 card numbers indicated. :)