Curated Tumblr

The problem with common core math was not that they taught these techniques. It's that they taught exclusively these techniques. These techniques are born from the meta manipulation of the numbers which comes when you have an understanding of the logic of arithmetic and see the patterns and how they can be manipulated. You need to understand why you can you "borrow" 1 from the 7 or the 9 to the other number and get the same answer, for example. It makes arithmetic easier for those who do it, yes, but only because we understand why you are doing it that way.

When you just teach the meta manipulation, the technique, without the reason, you are teaching a process that has no foundation. The smarter kids may learn to understand the foundational logic from that, but many will only memorize the rules they are taught without that understanding of why and then struggle to build more knowledge without that foundation later.

Math is a subject where each successive lesson is built on the previous lessons. Without being solid on your understanding, it is a house of cards waiting to fall.

There's ~~people~~aliens who would add 9+7 instead of 10+6 or 8+8 in their heads?

Well, there are certainly wrong ways to arrive at the answer, e.g. calculating 2+2 by multiplying both numbers still gets you 4 but that is the wrong way to get there. That doesn't apply to any of the methods in the post though.

Unsolved problems do not all fall into binary outcomes. They can be independent of axioms (the set of assumptions used to construct a proof).

Nothing, it has become quite common to say ADHD causes every little odd behavior. I'm not sure if all those people are even actually diagnosed and not just lying for internet points...

I assume people with actual ADHD find it offensive their condition is made fun of by "quirky" idiots online.

ADHD is sometimes used as a catchall to mean a set of behaviors that does not coincide with the majority at school or work. Ive met a bunch of people on ADHD medicine, but it was usually because they wanted to force themselves to be good at or like something they didnt want to do normally.

In this case its called ADHD because the student has found their own way to solve it despite the method the teacher is teaching and that the rest of the class uses.

Wouldn't say nothing to do with.
Many neurodivergent students find themselves in situations where they haven't fully absorbed the taught material. Many of them end up figuring problems out themselves, with varying degrees of creativity and success

Yeah, this has nothing to do with ADHD.

I'd argue memorizing it is the natural way, at least if you work with numbers a lot. Think about how a typist can type a seven letter word faster than a string of seven random characters. Is that not good proof that we have pathways in our brain that short circuit simpler procedural steps?

Yup, this is what parents are complaining about when they say math has changed. Before, math was primarily about rote memorization. You just memorized that 9+7 is 16. There were multiplication tables you were expected to memorize and regurgitate ad nauseam. Sure you could count it out on your fingers, but that only works for numbers under 11. For anything above that, you just referred to your memorized addition, subtraction, multiplication, or division tables. But this also meant that numbers outside of those tables were really difficult to do in your head, because you were poorly equipped to actually calculate them out.

Common core math is attempting to make math easier to do in your head, by teaching the concepts (rather than promoting rote memorization) and helping students learn shortcuts to avoid getting lost. 9+7 is 16, but it’s also 10+6 or 8*2, which are much easier to visualize in your head without counting on your fingers.

Admittedly I was in school multiple decades ago, but our teachers wanted us to memorize addition and multiplication tables. Which of course made anything outside the tables hard to do. I (and others apparently) thought it would be a great idea to use shortcuts like this.

So many failed tests. So many. When teachers saw us write down that we took the 21 apples multiplied by 7 bushels and just did 2x7, and tack a 7 on the end, they broke out the red pen.

My math teacher (at a private school) was just a random students' mom. She had no higher degree and only taught the book. If you got the right answer by using a method not included in the book, it was marked half-credit because she didn't understand and wasn't interested in hearing your logic, because "that's not what the book says".

Being taught by people who have no drive for knowledge and just want to teach the standardized test answers SUCKS.

I had to memorize multiplication. We weren't taught any other way. 3x3 = 9 because it just is that way, memorize it. I had stacks of flash cards. My mom struggled so hard for weeks to teach me my multiplication tables at home. In the end, I (somehow) passed the multiplication quiz or whatever and did my best to do as little multiplication as I could for the rest of my life. As a result, I still have never learned all the multiplication tables, and have a deep dislike of math or numbers in general.

I bet my education would have been a lot different if I could have learned how to multiply effectively from a young age.

And the reason they teach it that way is because it’s what the people who are good at math were already doing. Math isn’t about memorization it’s about understanding how numbers work and that’s how numbers work

If anything, these are exactly the techniques that "New Math" was supposed to teach. Your brain doesn't work math the same way as a computer. People who are good at math tend to break the whole thing down into simple pieces like this. New Math was developed by studying what they did and then teaching that to everyone.

I tend to add 9 to things by bumping the tens digit up by one (7 becomes 17) and then subtracting 1 (17 becomes 16).

Most of the arguments against New Math tended to prove the point; our mathematical education was in dire need of fixing.

9 plus a number? No. 10 plus a number, minus 1. Yis.

I thought that too, 9 is like a halogen, it wants to resolve to 10 anyway it can like fluorine wants one last electron. So allow the 9 to rip one off of the neighboring numbers and then perform the calculation.

In my school they encouraged you to come up with techniques like this.

You’re either very lucky and were in a school that went against established norms, or you’re young enough that you were taught the “new” math that boomers hate. Because this is the new math.

Boomers, GenX, and elder millennials were primarily taught via rote memorization. You simply memorized the times tables, and committed “8*3=24” to memory. You didn’t calculate it every time. You just memorized the tables, regurgitated them ad nauseam to appease the teachers, and then referred to those memorized tables for any multiplication you needed to do.

For reference, this is the times table I’m referring to. Our quizzes/tests required you to fill out the entire thing in less than 5 minutes:

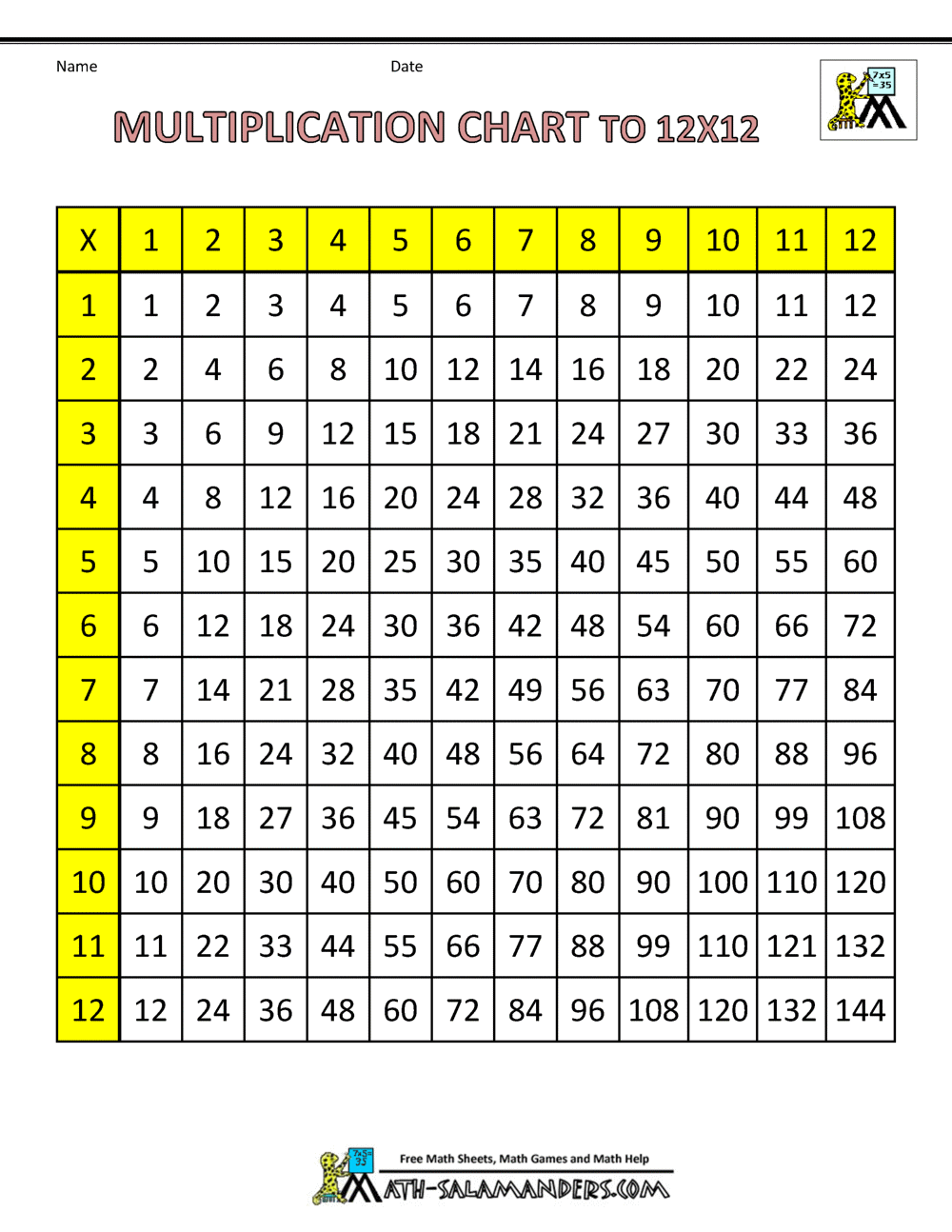
We had to fill this out multiple times per week. The goal of the time limit was to force you to memorize it, instead of calculating it out every time. You simply didn’t have time to calculate each one out. Then once you had it memorized, if you ever had to do 8*3, you would just refer to your memorized times tables for it.

But the issue with this is that it doesn’t teach you how to actually do the math in your head, it just teaches you the times tables. You aren’t calculating it out each time, so you don’t develop any shortcuts or methods to make it easier. If a teacher ever saw you turn 9+7 into 10+6, they would bust out the red pen and start slashing. Even though 10+6 is undeniably easier to do in your head, the teachers weren’t concerned with that; They wanted to know that you had memorized what 9+7 is. These memes are primarily aimed at the millennials and GenX with ADHD, because they were the ones who got bored of rote memorization and started coming up with shortcuts (which then got docked points on their quizzes.)

Probably because they were forced to memorize times tables, but not arithmetic so they wanted to show where they are leveraging that memorization from