this post was submitted on 24 Jul 2023
18 points (95.0% liked)
Astronomy
4122 readers
34 users here now
founded 3 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
Using the Lorenz transformation formula, here's what I get:
In the Earth's reference frame, the planet starts at (t=0,x=0) and just stays still for time T (say 4.5 billion years):
In the spaceship's prime frame, we get:
I think your problem was you forgot the γ factor, which is still present even when using natural units. Or as the wiki describes it: "As illustrated in Fig 2-3, the boosted and unboosted spacetime axes will in general have unequal unit lengths."
Edit: oh wait, you would still be upset that t' = γT > T = t. Ok then! So using this diagram for example, two time units pass between O and P along the Earth's red time axis, but 3 time units pass along the spaceship's green prime time axis, and this is in conflict with the article's claim that the Earth's frame is the frame with the maximum rate of time.
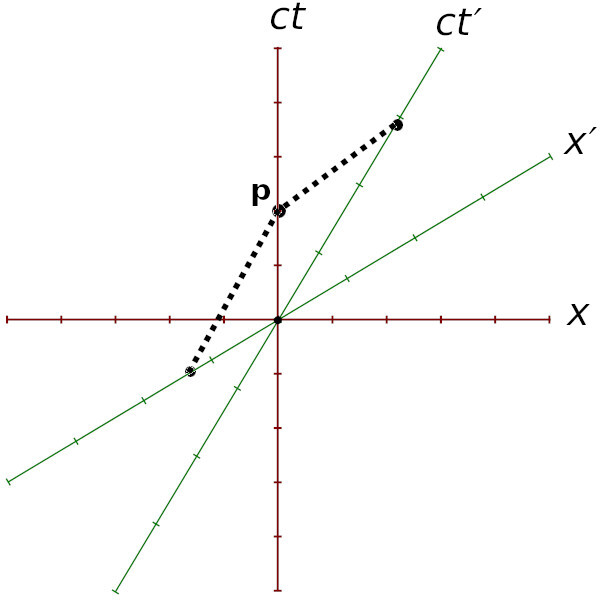
I think the author meant to say you should calculate the time elapsed along the path that ends up back at the same point. If the spaceship were to turn around and return, 6 time units will have elapsed for it here, but 7 time units on earth. I.e. we are in the Twin's Paradox/relativity of simultaneity territory here, but the important thing is that there is no path for the spaceship where you would see 7 or more time units elapsed, other than staying on Earth.
Thanks, I think we are actually in agreement here: if you account for the fact that
\gamma > 1in general, then your calculation showed thatT' = \gamma T > T, that is, the moving observer in general registers a longer durationT'between the two events than the clock at rest (T). I was just taking a shortcut when I said this should follow fromX' != 0(the-\gamma v Tin your calculation).Also, thanks for the imagery of aliens taking earth for a joy ride. This might be how we are saved when the sun dies.
Edit: I think we agree on both accounts as the twin paradox is also the only way I can rationalize the original claim (even said so in my first reply)
The fact that there is a maximum amount of relative time that can elapse between any 2 "events" does not rely on the twin paradox in any way. It doesn't even depend on movement at all since there is gravitational time dilation and the 2 events don't even need to be "witnessed" for time to have a particular relative duration between the events. Whichever of 2 different inertial frames of reference has the least amount of gravitational time dilation has the faster time flow rate and is closest to the maximum rate.
If a piece of matter had no gravitational time dilation at all (which admittedly is impossible) what would be the time flow rate for the object? For simplicity let's assume it is not accelerating or even moving at all (except for expansion of universe). How would we know it is not moving? Let's assume (call it a thought experiment) that the universe has a center and boundaries, and that the distance and direction to the center is not changing. This object would have no time dilation, the maximum time flow rate, and experience the longest possible duration of time across any arbitrary points in time.
That was exactly the point, although I think there are also other ways to prove it. Thanks for expressing this better than I.