User @[email protected] has posed a challenge when trying to argue that... wait, what?
The biggest, if rarely used, use case [of LLMs] is education - they’re an infinitely patient tutor that can explain things in many ways and give you endless examples.
Lol what.
Try reading something like Djikstra’s algorithm on Wikipedia, then ask one to explain it to you. You can ask for a theme, ask it to explain like you’re 5, or provide an example to check if you understood and have it correct any mistakes
It’s fantastic for technical or dry topics, if you know how to phrase things you can get quick lessons tailored to be entertaining and understandable for you personally. And of course, you can ask follow up questions
Well, usually AI claims are just unverifiable gibberish but this? Dijkstra's algorithm is high school material. This is a verifiable claim. And oh boi, do AI claims have a long and storied history of not standing up to scrutiny...
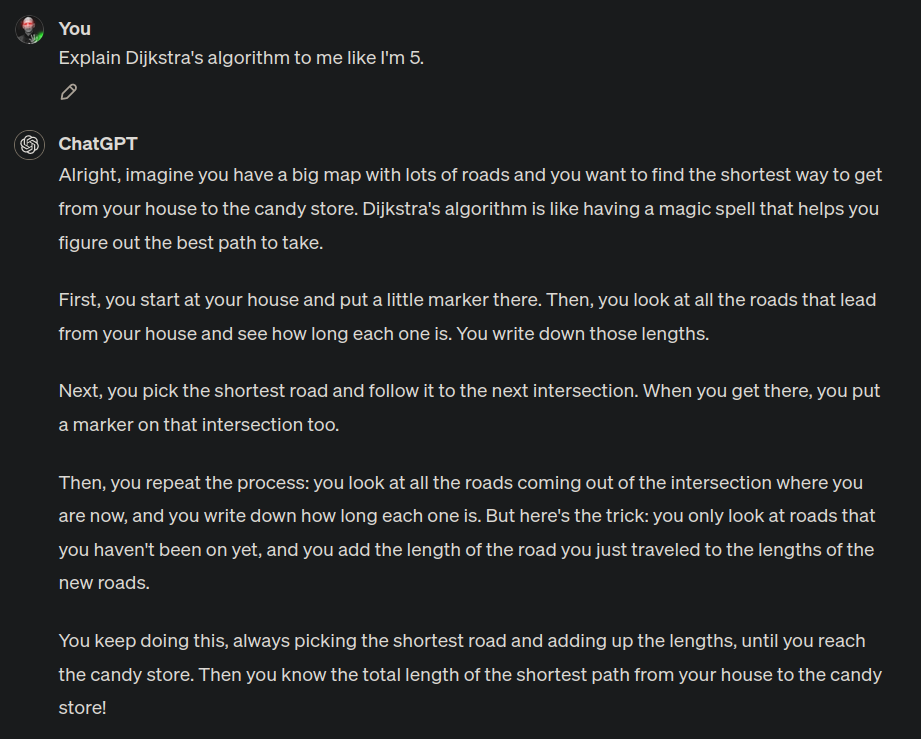
Transcript
Me: Explain Dijkstra's algorithm to me like I'm 5. ChatGPT: Alright, imagine you have a big map with lots of roads and you want to find the shortest way to get from your house to the candy store. Dijkstra's algorithm is like having a magic spell that helps you figure out the best path to take.
First, you start at your house and put a little marker there. Then, you look at all the roads that lead from your house and see how long each one is. You write down those lengths.
Next, you pick the shortest road and follow it to the next intersection. When you get there, you put a marker on that intersection too.
Then, you repeat the process: you look at all the roads coming out of the intersection where you are now, and you write down how long each one is. But here's the trick: you only look at roads that you haven't been on yet, and you add the length of the road you just traveled to the lengths of the new roads.
You keep doing this, always picking the shortest road and adding up the lengths, until you reach the candy store. Then you know the total length of the shortest path from your house to the candy store!
I sincerely didn't expect it'd take me so little, but well, this is patently wrong. One, this is not Dijkstra's algorithm. Two, picking the shortest road always is obviously incorrect, see this map:
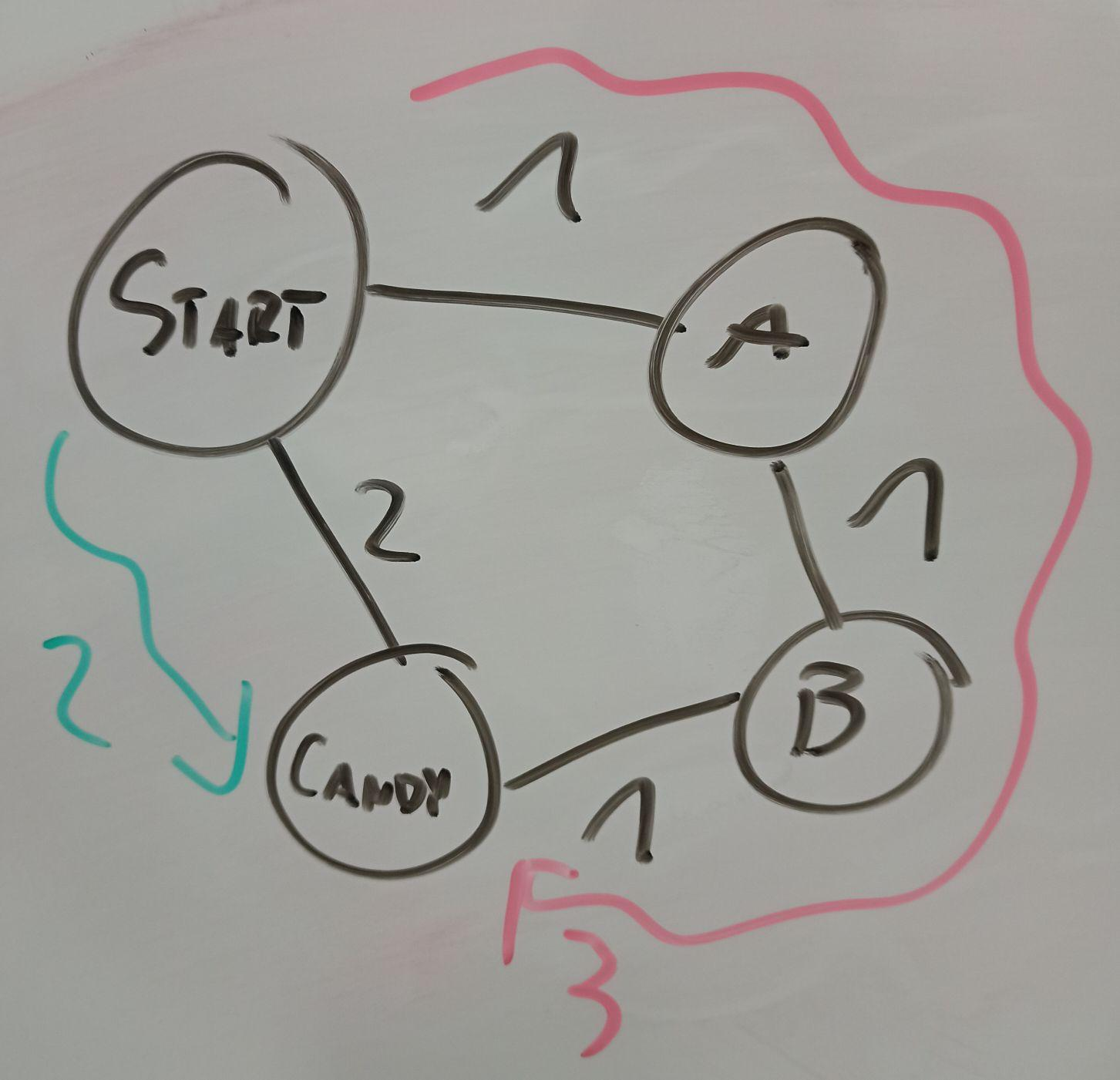
Green path is the shortest to candy. Red path is what you get by always following the shortest road.
Dijkstra's algorithm picks the closest node that was seen thus far and tries to make paths better by expanding from there, the idea being that if some node is far away then paths through it are going to be long, so we don't need to look at them until there's no other option. In this case it'll immediately see A at distance 1 and Candy at distance 2, expand from A (since it's closer) to get to B in distance 2; after that it will look at B and Candy, but see it cannot improve from there and terminate.
Let's see what ChatGPT will tell me when I bring this counterexample to its stupid algorithm to its attention.
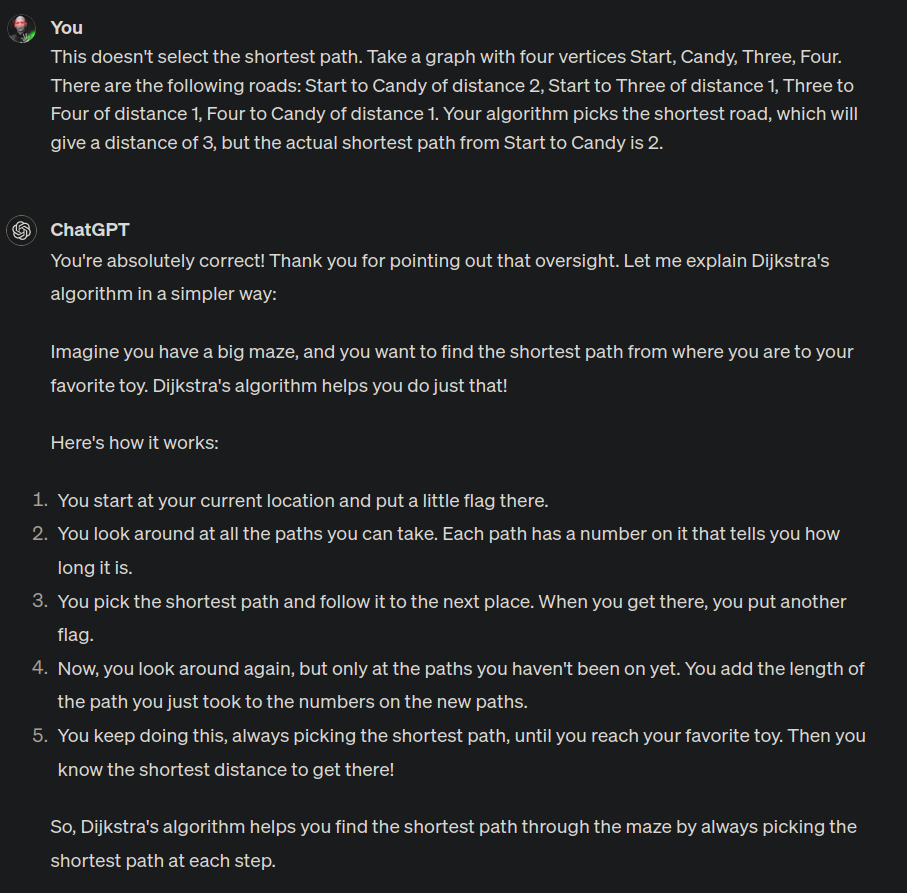
Transcript
Me: This doesn't select the shortest path. Take a graph with four vertices Start, Candy, Three, Four. There are the following roads: Start to Candy of distance 2, Start to Three of distance 1, Three to Four of distance 1, Four to Candy of distance 1. Your algorithm picks the shortest road, which will give a distance of 3, but the actual shortest path from Start to Candy is 2.
ChatGPT: You're absolutely correct! Thank you for pointing out that oversight. Let me explain Dijkstra's algorithm in a simpler way:
Imagine you have a big maze, and you want to find the shortest path from where you are to your favorite toy. Dijkstra's algorithm helps you do just that!
Here's how it works:
- You start at your current location and put a little flag there.
- You look around at all the paths you can take. Each path has a number on it that tells you how long it is.
- You pick the shortest path and follow it to the next place. When you get there, you put another flag.
- Now, you look around again, but only at the paths you haven't been on yet. You add the length of the path you just took to the numbers on the new paths.
- You keep doing this, always picking the shortest path, until you reach your favorite toy. Then you know the shortest distance to get there!
So, Dijkstra's algorithm helps you find the shortest path through the maze by always picking the shortest path at each step.
It fucking doubles down! It says it's wrong and then gives the same stupid algorithm just with "map" changed to "maze" and "candy" changed to "toy"! And I wanted candy!
Okay, maybe saying "like I'm 5" was wrong, let's try to recreate something closer to what @theneverfox wanted.

Transcript
Me: I read the wikipedia article on Dijkstra's algorithm but didn't understand it. Can you explain it to me? Of course! Dijkstra's algorithm is a fundamental method used in computer science for finding the shortest paths between nodes in a graph, particularly for graphs with non-negative edge weights. It was developed by Dutch computer scientist Edsger W. Dijkstra in 1956.
Here's a simplified explanation of how Dijkstra's algorithm works:
- Initialization: Start at a chosen source node and mark its distance as 0. Mark the distances to all other nodes as infinity (or a very large number). Also, create an empty set to keep track of visited nodes and a priority queue (often implemented using a min-heap) to prioritize nodes to visit next based on their current distances. 2.Iterative Process: Repeat the following steps until all nodes have been visited:
- Choose the unvisited node with the smallest known distance from the source.
- For the current node, consider all of its unvisited neighbors and calculate their tentative distances through the current node. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one. For example, if the current node is A and the neighbor B, calculate the distance to B through A and compare it to the previously known distance to B. If it's smaller, update the distance to B.
- Mark as Visited: Once all of the neighbors of the current node have been considered, mark the current node as visited and remove it from the unvisited set.
- Termination: The algorithm terminates when all nodes have been visited, or if the smallest tentative distance among the unvisited nodes is infinity. This happens when there is no connection between the initial node and remaining unvisited nodes.
- Path Reconstruction (optional): If you also need to find the shortest path from the source node to a target node, you can track the predecessors of each node during the algorithm execution. Once the algorithm terminates, you can backtrack from the target node to the source node using the predecessors to reconstruct the shortest path.
Dijkstra's algorithm is guaranteed to find the shortest path from the source node to all other nodes in the graph, as long as the graph doesn't contain any negative-weight cycles (cycles where the total weight of the edges is negative). If there are negative weights, you'd typically use the Bellman-Ford algorithm instead.
Okay, at least it's not incorrect, there are no lies in this, although I would nitpick two things:
- It doesn't state what the actual goal of the algorithm is. It says "fundamental method used in computer science for finding the shortest paths between nodes in a graph", but that's not precise; it finds the shortest paths from a node to all other nodes, whereas the wording could be taken to imply its between two nodes.
- "infinity (or a very large number)" is very weird without explanation. Dijkstra doesn't work if you put "a very large number", you have to make sure it's larger than any possible path length (for example, sum of all weights of edges would work).
Those are rather pedantic and I can excuse them. The bigger issue is that it doesn't really tell you anything that you wouldn't get from the Wikipedia article? It lifts sentences from there changing the structure, but it doesn't make it any clearer. Actually, Wikipedia has an example in the text describing the "Iterative Process" steps, but ChatGPT threw it away. What's the value here, exactly?
Let's try asking something non-obvious that I didn't get first when learning Dijkstra:

Transcript
Me: Why does Dijkstra not work if edges have negative weights? ChatGPT: Dijkstra's algorithm relies on the assumption that adding a new edge to the current path cannot make the path shorter than it already is. In other words, it assumes that the sum of edge weights along any path is non-decreasing. This property is crucial for the correctness of Dijkstra's algorithm. When negative weights are present in the graph, this assumption no longer holds true. If there's a negative-weight edge between two nodes, it becomes possible to construct a path that's shorter than any previously known path. As a result, Dijkstra's algorithm can fail to find the correct shortest paths or may even enter into an infinite loop if negative-weight cycles are present. Consider the following scenario:
- You have a graph with two nodes A and B connected by an edge with weight -1.
- You start Dijkstra's algorithm at node A.
- Dijkstra's algorithm greedily chooses the shortest path available at each step. In this case, it would immediately choose the edge with weight -1 to reach node B.
- Now, the distance to node B becomes -1, which is less than any other edge weight you might encounter later.
- As a result, Dijkstra's algorithm might incorrectly conclude that the shortest path from A to B has been found, even though it's actually not true. To handle graphs with negative weights or negative-weight cycles, you need more sophisticated algorithms like the Bellman-Ford algorithm, which can correctly handle these cases by relaxing edges multiple times and detecting negative-weight cycles. Me: Can you give a better counterexample? ChatGPT: Sure, let's consider a counterexample where Dijkstra's algorithm fails due to negative weights. Imagine a graph with three nodes A, B, and C, connected as follows:
- A to B with weight 1
- A to C with weight 4
- B to C with weight -2 Let's say we want to find the shortest path from A to C. Here's what happens with Dijkstra's algorithm:
- Start at node A, mark its distance as 0 and all other nodes' distances as infinity.
- Visit node A. Update the distances of its neighbors:
- Distance to B: 1 (via A)
- Distance to C: 4 (via A)
- Visit node B. Update the distance to C:
- Distance to C: 1 (via B) Visit node C. Since all nodes are visited, the algorithm terminates.
According to Dijkstra's algorithm, the shortest path from A to C is through B, with a distance of 1. However, this is incorrect because it fails to consider the negative weight from B to C.
The actual shortest path from A to C is directly from A to C with a distance of 4. So, in this case, Dijkstra's algorithm fails to find the correct shortest path due to the presence of negative weights.
What?! This is nonsense! Gibberish! Bollocks!
It does really well at first, no wonder, since the first sentences are regurgitated from Wikipedia. Then it gives a frankly idiotic example of a two vertex graph where Dijkstra does give the correct answer since it's trivial and there's only one edge. But it's really easy to come up with an actual counterexample, so I asked for it directly, and got... Jesus Christ. If images are better for you, here is the graph described by ChudGPT:
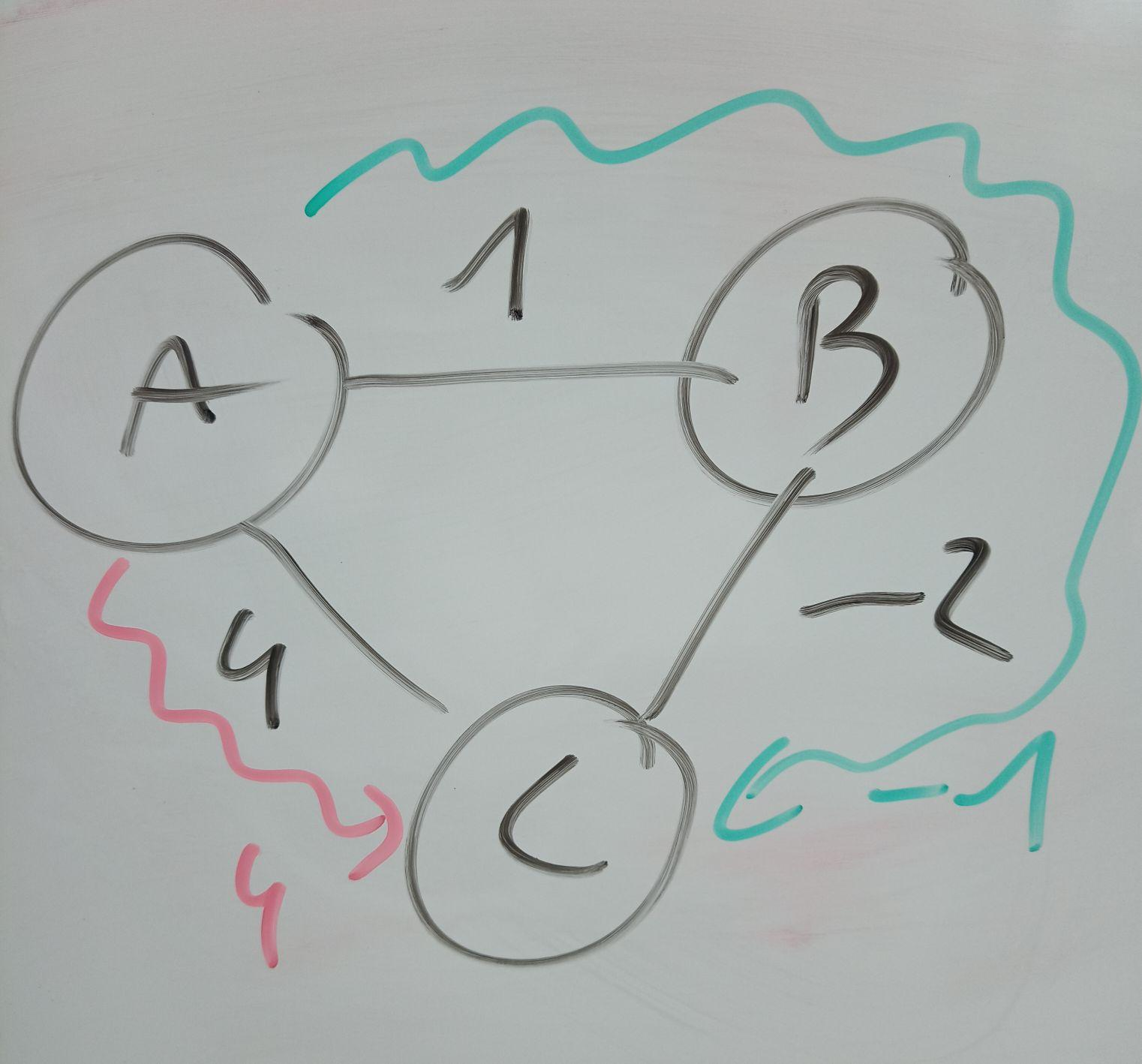
Dijkstra here correctly picks the shortest path to C:
- Distances = { 0, ∞, ∞ }, active = [A at 0], pick edges from A
- Distances = { 0, 1, 4 }, active = [B at 1, C at 4], pick edges from B
- Distances = { 0, 1, -1 }, active = [C at -1], pick edges from C
- Distances = { 0, 1, -1 }, end.
This is not a counterexample to Dijkstra. ChatGPT even says that! Its step 3 clearly finds the distance 1 to C! And then it says the actual shortest path is 4! A fucking 7 year old can see this is wrong!
It's very easy to change this to an actual counterexample as well, just replace the weight on A->B with 5. The shortest path is then 3, but because of how Dijkstra works it will visit C first, save the distance of 4, and then never revisit C. This is the actual reason Dijkstra doesn't work.
It fails miserably to explain the basics, it fails spectacularly to explain a non-obvious question an actual student just introduced to Dijkstra might have, and, I left my specialité for the end:

Transcript
Me: Can I use Dijkstra to find the longest path from A to B? ChatGPT: No, Dijkstra's algorithm is specifically designed to find the shortest paths in a graph. It's not directly applicable to finding the longest path between two nodes. The reason lies in the nature of Dijkstra's algorithm itself. It relies on the principle of greedily selecting the shortest path at each step. This greedy approach ensures that once a node is visited and its shortest path is determined, it will never be revisited. Consequently, it's not suitable for finding the longest path, as it doesn't consider the possibility of revisiting nodes or taking longer paths. Finding the longest path in a graph is a more complex problem and typically involves different algorithms or approaches. One common method is to transform the problem into finding the shortest path by negating the weights of all edges and then applying Dijkstra's algorithm. However, this approach only works for acyclic graphs, as negating the weights can't handle cycles. For finding the longest path in a general graph, you would need to use more specialized algorithms, such as topological sorting combined with dynamic programming or algorithms specifically designed for longest path problems, like the Floyd-Warshall algorithm with modifications. These methods can handle cycles and provide the correct longest path in the graph.
More computer-science-savvy among you are surely already laughing. ChatGPT just solved P=NP! With Floyd-Warshall!
Again, it starts off good -- Dijkstra indeed cannot find longest paths. The next sentence is technically correct, though rather hollow.
"Finding the longest path in a graph is a more complex problem and typically involves different algorithms or approaches." Ye, that's correct, it's extremely complex -- it's what we call an NP-complete problem ^1^! It's currently unknown whether these problems are solvable in reasonable time. It then gives the "negate the weights" approach and correctly remarks it doesn't actually work, and then it absolutely clowns itself by saying you can solve it with Floyd-Warshall. You can't. That's just plain dumb. How would it?
I'm not going to delve deeper into this. This is a bullshit generator that has a passing knowledge of the Wikipedia article (since it trained on it), but shows absolutely no understanding of the topic it covers. It can repeat the basic sentences it found, but it cannot apply them in any new contexts, it cannot provide sensible examples, it stumbles over itself when trying to explain a graph with three fucking vertices. If it were a student on an oral exam for Intro to Algorithms I would fail it.
And as a teacher? Jesus fucking Christ, if a guy stumbled into a classroom to teach first year students, told them that you can find shortest paths by greedily choosing the cheapest edge, then gave a counter-counterexample to Dijkstra, and finally said that you can solve Longest Path in O(n^3^), he better be also fucking drunk, cause else there'd be no excuse! That's malpractice!
None of this is surprising, ChudGPT is just spicy autocomplete after all, but apparently it bears laying out. The work of an educator, especially in higher education, requires flexibility of mind and deep understanding of the covered topics. You can't explain something in simple words if you don't actually get it, and you can't provide students with examples and angles that speak to them and help in their learning process if you don't understand the topic from all those angles yourself. LLMs can't do that, fundamentally and by design.
It’s fantastic for technical or dry topics
Give me a fucking break.
^1^. Pedantically, it's NP-hard, the decision version is NP-complete. This footnote is to prevent some smartass from correcting me in the comments...
One thing that would be a good addition to the recommended NSFW reading list would be an explanation of basic CS theory that's good enough to forestall the worst of the woo, or at least give a reader who isn't already a lost cause the tools to recognize the woo.